FUNÇÃO INVERSA

FUNÇÃO INVERSA - INTRODUÇÃO

A função inversa é um tipo de função bijetora (sobrejetora e injetora). Isso porque os elementos de uma função A possui um elemento correspondente de uma função B.

Sendo assim, é possível trocar os conjuntos e associar cada elemento de B com os de A.

A função inversa é representada por: f -1

Exemplo:

Dada as funções A = {1, 2, 3, 4} e B = {1, 3, 5, 7} e definida pela lei y = 2x – 1, temos:

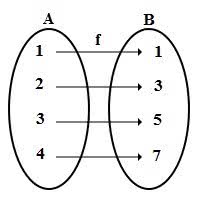
Logo,

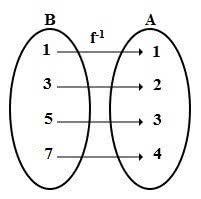
A função inversa f -1 é dada pela lei:

y = 2x – 1
y +1 = 2x
x = y + 1/2

FUNÇÃO COMPOSTA

FUNÇÃO COMPOSTA - INTRODUÇÃO

A função composta, também chamada de função de função, é um tipo de função matemática que combina duas ou mais variáveis.

Sendo assim, ela envolve o conceito de proporcionalidade entre duas grandezas, e que ocorre por meio de uma só função.

Dada uma função f (f: A → B) e uma função g (g: B → C), a função composta de g com f é representada por gof. Já a função composta de f com g é representada por fog.

fog (x) = f(g(x))
gof (x) = g(f(x))

Note que nas funções compostas as operações entre as funções não são comutativas. Ou seja, fog ≠ gof.

Assim, para resolver uma função composta aplica-se uma função no domínio de outra função. E, substitui-se a variável x por uma função.

Exemplo

Determine o gof(x) e fog(x) das funções f(x) = 2x + 2 e g(x) = 5x.

gof(x) = g[f(x)] = g(2x+2) = 5(2x+2) = 10x + 10
fog(x) = f[g(x)] = f(5x) = 2(5x) + 2 = 10x + 2

FUNÇÕES: INJETORA, BIJETORA E SOBREJETORA

CONCEITO DE FUNÇÃO BIJETORA

A função bijetora, também chamada de bijetiva, é um tipo de função matemática que relaciona elementos de duas funções.

Desse modo, os elementos de uma função A possuem correspondentes em uma função B. Importante notar que elas apresentam o mesmo número de elementos em seus conjuntos.

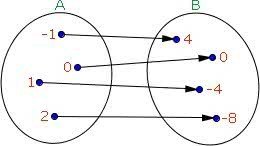
A partir desse diagrama, podemos concluir que:

O domínio dessa função é o conjunto {-1, 0, 1, 2}. O contradomínio reúne os elementos: {4, 0, -4, -8}. Já o conjunto imagem da função é definido por: Im(f) = {4, 0, -4, -8}.

A função bijetora recebe esse nome pois ela é injetora e sobrejetora ao mesmo tempo. Em outras palavras, uma função f: A → B é bijetora quando f é injetora e sobrejetora.

Na função injetora, todos os elementos da primeira têm como imagem elementos distintos da outra.

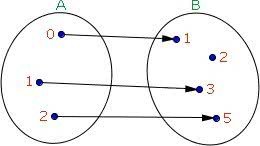
Já na função sobrejetora, todo elemento do contradomínio de uma função é imagem de pelo menos um elemento do domínio de outra.

Exemplos de Funções Bijetoras

Dada as funções A = {1, 2, 3, 4} e B = {1, 3, 5, 7} e definida pela lei y = 2x – 1, temos:

Vale notar que a função bijetora sempre admite uma função inversa (f -1). Ou seja, é possível inverter e relacionar os elementos de ambas:

Outros exemplos de funções bijetoras:

f: R → R tal que f(x) = 2x
f: R → R tal que f(x) = x3
f: R+ → R+ tal que f(x) = x2
f: R* → R* tal que f(x) = 1/x

Gráfico Função Bijetora

Confira abaixo o gráfico de uma função bijetora f(x) = x + 2, onde f: [1; 3] → [3; 5]:

CONCEITO DE FUNÇÃO SOBREJETORA

A função sobrejetora, também chamada de sobrejetiva é um tipo de função matemática que relaciona elementos de duas funções.

Na função sobrejetora, todo elemento do contradomínio de uma é imagem de pelo menos um elemento do domínio de outra.

Em outras palavras, numa função sobrejetora o contradomínio é sempre igual ao conjunto imagem.

f: A → B, ocorre a Im(f) = B

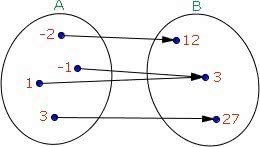
No diagrama acima temos que o domínio dessa função sobrejetora reúne os elementos {-2, -1, 1, 3}. Já o contradomínio é o conjunto representado por {12, 3, 27} e o conjunto imagem é {12, 3, 27}.

Gráfico da Função Sobrejetora

No gráfico de uma função sobrejetora notamos que a imagem da função é igual a B: Im(f) = B.