A função bijetora, também chamada de bijetiva, é um tipo de função matemática que relaciona elementos de duas funções.
Desse modo, os elementos de uma função A possuem correspondentes em uma função B. Importante notar que elas apresentam o mesmo número de elementos em seus conjuntos.
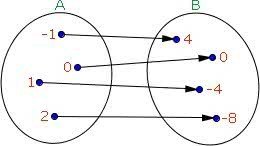
A partir desse diagrama, podemos concluir que:
O domínio dessa função é o conjunto {-1, 0, 1, 2}. O contradomínio reúne os elementos: {4, 0, -4, -8}. Já o conjunto imagem da função é definido por: Im(f) = {4, 0, -4, -8}.
A função bijetora recebe esse nome pois ela é injetora e sobrejetora ao mesmo tempo. Em outras palavras, uma função f: A → B é bijetora quando f é injetora e sobrejetora.
Na função injetora, todos os elementos da primeira têm como imagem elementos distintos da outra.
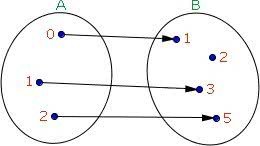
Já na função sobrejetora, todo elemento do contradomínio de uma função é imagem de pelo menos um elemento do domínio de outra.
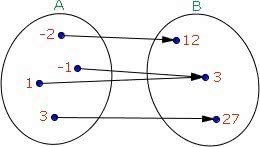
Exemplos de Funções Bijetoras
Dada as funções A = {1, 2, 3, 4} e B = {1, 3, 5, 7} e definida pela lei y = 2x – 1, temos:
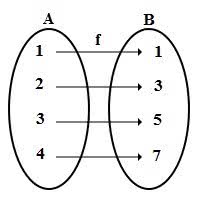
Vale notar que a função bijetora sempre admite uma função inversa (f -1). Ou seja, é possível inverter e relacionar os elementos de ambas:
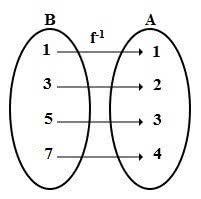
Outros exemplos de funções bijetoras:
f: R → R tal que f(x) = 2x
f: R → R tal que f(x) = x3
f: R+ → R+ tal que f(x) = x2
f: R* → R* tal que f(x) = 1/x
f: R → R tal que f(x) = x3
f: R+ → R+ tal que f(x) = x2
f: R* → R* tal que f(x) = 1/x
Gráfico Função Bijetora
Confira abaixo o gráfico de uma função bijetora f(x) = x + 2, onde f: [1; 3] → [3; 5]:


Nenhum comentário:
Postar um comentário