sexta-feira, 20 de abril de 2018
FUNÇÃO INVERSA - INTRODUÇÃO
A função inversa é um tipo de função bijetora (sobrejetora e injetora). Isso porque os elementos de uma função A possui um elemento correspondente de uma função B.
Sendo assim, é possível trocar os conjuntos e associar cada elemento de B com os de A.
A função inversa é representada por: f -1

Exemplo:
Dada as funções A = {1, 2, 3, 4} e B = {1, 3, 5, 7} e definida pela lei y = 2x – 1, temos:
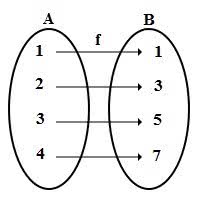
Logo,
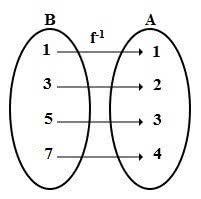
A função inversa f -1 é dada pela lei:
y = 2x – 1
y +1 = 2x
x = y + 1/2
y +1 = 2x
x = y + 1/2
FUNÇÃO COMPOSTA - INTRODUÇÃO
A função composta, também chamada de função de função, é um tipo de função matemática que combina duas ou mais variáveis.
Sendo assim, ela envolve o conceito de proporcionalidade entre duas grandezas, e que ocorre por meio de uma só função.
Dada uma função f (f: A → B) e uma função g (g: B → C), a função composta de g com f é representada por gof. Já a função composta de f com g é representada por fog.
fog (x) = f(g(x))
gof (x) = g(f(x))
gof (x) = g(f(x))

Note que nas funções compostas as operações entre as funções não são comutativas. Ou seja, fog ≠ gof.
Assim, para resolver uma função composta aplica-se uma função no domínio de outra função. E, substitui-se a variável x por uma função.
Exemplo
Determine o gof(x) e fog(x) das funções f(x) = 2x + 2 e g(x) = 5x.
gof(x) = g[f(x)] = g(2x+2) = 5(2x+2) = 10x + 10
fog(x) = f[g(x)] = f(5x) = 2(5x) + 2 = 10x + 2
fog(x) = f[g(x)] = f(5x) = 2(5x) + 2 = 10x + 2
CONCEITO DE FUNÇÃO BIJETORA
A função bijetora, também chamada de bijetiva, é um tipo de função matemática que relaciona elementos de duas funções.
Desse modo, os elementos de uma função A possuem correspondentes em uma função B. Importante notar que elas apresentam o mesmo número de elementos em seus conjuntos.
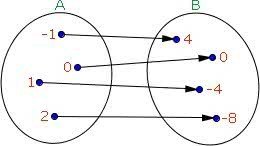
A partir desse diagrama, podemos concluir que:
O domínio dessa função é o conjunto {-1, 0, 1, 2}. O contradomínio reúne os elementos: {4, 0, -4, -8}. Já o conjunto imagem da função é definido por: Im(f) = {4, 0, -4, -8}.
A função bijetora recebe esse nome pois ela é injetora e sobrejetora ao mesmo tempo. Em outras palavras, uma função f: A → B é bijetora quando f é injetora e sobrejetora.
Na função injetora, todos os elementos da primeira têm como imagem elementos distintos da outra.
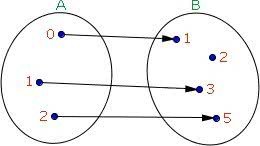
Já na função sobrejetora, todo elemento do contradomínio de uma função é imagem de pelo menos um elemento do domínio de outra.
Exemplos de Funções Bijetoras
Dada as funções A = {1, 2, 3, 4} e B = {1, 3, 5, 7} e definida pela lei y = 2x – 1, temos:

Vale notar que a função bijetora sempre admite uma função inversa (f -1). Ou seja, é possível inverter e relacionar os elementos de ambas:

Outros exemplos de funções bijetoras:
f: R → R tal que f(x) = 2x
f: R → R tal que f(x) = x3
f: R+ → R+ tal que f(x) = x2
f: R* → R* tal que f(x) = 1/x
f: R → R tal que f(x) = x3
f: R+ → R+ tal que f(x) = x2
f: R* → R* tal que f(x) = 1/x
Gráfico Função Bijetora
Confira abaixo o gráfico de uma função bijetora f(x) = x + 2, onde f: [1; 3] → [3; 5]:

CONCEITO DE FUNÇÃO SOBREJETORA
A função sobrejetora, também chamada de sobrejetiva é um tipo de função matemática que relaciona elementos de duas funções.
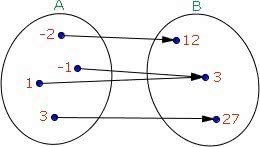
Na função sobrejetora, todo elemento do contradomínio de uma é imagem de pelo menos um elemento do domínio de outra.
Em outras palavras, numa função sobrejetora o contradomínio é sempre igual ao conjunto imagem.
f: A → B, ocorre a Im(f) = B
No diagrama acima temos que o domínio dessa função sobrejetora reúne os elementos {-2, -1, 1, 3}. Já o contradomínio é o conjunto representado por {12, 3, 27} e o conjunto imagem é {12, 3, 27}.
Gráfico da Função Sobrejetora
No gráfico de uma função sobrejetora notamos que a imagem da função é igual a B: Im(f) = B.

CONCEITO DE FUNÇÃO INJETORA
A função injetora, também chamada de injetiva, é um tipo de função que apresenta elementos correspondentes em outra.
Assim, dada uma função f (f: A → B), todos os elementos da primeira têm como imagem elementos distintos de B. No entanto, não há dois elementos distintos de A com a mesma imagem de B.

Exemplo
Dada funções: f de A = {0, 1, 2, 3} em B = {1, 3, 5, 7, 9} definida pela lei f(x) = 2x + 1. No diagrama temos:

Observe que todos os elementos da função A possui correspondentes em B, no entanto, um deles não está correspondido (9).
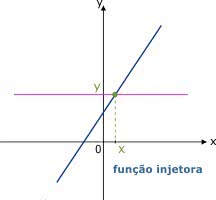
Gráfico
Na função injetora, o gráfico pode ser crescente ou decrescente. Ele é determinado por uma reta horizontal que passa por um único ponto. Isso porque um elemento da primeira função possui um correspondente na outra.
CONCEITO DE PLANO CARTESIANO
O Plano Cartesiano é formado por dois eixos perpendiculares: um horizontal (abscissa) e outro vertical (ordenada).
O Sistema de Coordenadas Cartesianas, mais conhecido como Plano Cartesiano foi criado por René Descartes com o objetivo de localizar pontos. Ele é formado por dois eixos perpendiculares: um horizontal e outro vertical que se cruzam na origem das coordenadas. O eixo horizontal é chamado de abscissa (x) e o vertical de ordenada (y). Os eixos são enumerados compreendendo o conjunto dos números reais. Observe a seguir uma figura representativa do plano cartesiano:
As coordenadas cartesianas são representadas pelos pares ordenados (x; y). Em
razão dessa ordem, devemos localizar o ponto observando primeiramente o eixo x
e posteriormente o eixo y. Qualquer ponto que não se encontrar sobre os eixos,
estará localizado nos quadrantes, veja:
1º
quadrante = x > 0 e y > 0
2º quadrante = x < 0 e y > 0
3º quadrante = x < 0 e y < 0
4º quadrante = x > 0 e y < 0
2º quadrante = x < 0 e y > 0
3º quadrante = x < 0 e y < 0
4º quadrante = x > 0 e y < 0
Localizando pontos no Plano Cartesiano:
A(4; 3) → x = 4 e y = 3
B(1; 2) → x = 1 e y = 2
C(–2; 4) → x = –2 e y = 4
D(–3; –4) → x = –3 e y = –4
E(3; –3) → x = 3 e y = –3
O Plano Cartesiano é muito utilizado na construção de gráficos
de funções, onde os valores relacionados à x constituem o domínio e os valores
de y, a imagem da função. A criação do Sistema de Coordenadas Cartesianas é
considerada uma ferramenta muito importante na Matemática, facilitando a
observação do comportamento de funções em alguns pontos considerados críticos.
Podemos associar o Plano Cartesiano com a latitude e a
longitude, temas relacionados aos estudos geográficos e à criação do atual
sistema de posicionamento, o GPS. O Sistema de Posicionamento Global permite
que saibamos nossa localização exata na terra, desde que tenhamos em mão um
receptor de sinais GPS, informando a latitude, a longitude e a altitude com o
auxilio de satélites em órbita da Terra. Um exemplo de utilização do GPS são os
aviões, que para não se colidirem são monitorados e informados em qual rota
devem seguir viagem.
terça-feira, 17 de abril de 2018
FUNÇÕES: DOMÍNIO, CONTRADOMÍNIO E CONJUNTO IMAGEM
Função é uma expressão matemática que relaciona dois valores pertencentes a conjuntos diferentes, mas com relações entre si. A lei de formação que intitula uma determinada função, possui três características básicas: domínio, contradomínio e imagem. Essas características podem ser representadas por um diagrama de flechas, isso facilitará o entendimento por parte do estudante. Observe:
Dada a seguinte função f(x) = x + 1, e os conjuntos A(1, 2, 3, 4, 5) e B(1, 2, 3, 4, 5, 6, 7). Vamos construir o diagrama de flechas:
Dada a seguinte função f(x) = x + 1, e os conjuntos A(1, 2, 3, 4, 5) e B(1, 2, 3, 4, 5, 6, 7). Vamos construir o diagrama de flechas:
A
|
B
|
x
|
f(X)
|
1
|
2
|
2
|
3
|
3
|
4
|
4
|
5
|
5
|
6
|
Nessa situação, temos que:
Domínio: representado por todos os elementos do conjunto A.
(1, 2, 3, 4, 5)
Contradomínio: representado por todos os elementos do conjunto B.
(1, 2, 3, 4, 5, 6, 7)
Imagem: representada pelos elementos do contradomínio (conjunto B) que possuem correspondência com o domínio (conjunto A).
(2, 3, 4, 5, 6)
O conjunto domínio possui algumas características especiais que definem ou não uma função. Observe:
Todos os elementos do conjunto domínio devem possuir representação no conjunto do contradomínio. Caso isso não ocorra, a lei de formação não pode ser uma função.
Função
Não é uma função
Um único elemento do domínio não deve possuir duas imagens.
Não é função

Não é função
Um elemento do domínio não pode possuir duas imagens distintas.
Não é Função
Restam elementos no conjunto domínio, que não foram associados ao conjunto imagem.
CONCEITO DE FUNÇÕES
INTRODUÇÃO
Queremos estabelecer um exemplo motivacional para o estudo de funções, e nada melhor que estudar a relação existente entre as grandezas espaço e tempo. Queremos concluir que o espaço percorrido pode ser obtido como função do tempo gasto por um atleta, conforme descrito abaixo.
Exemplo: Numa esteira ergométrica, um atleta treina com uma velocidade constante para uma maratona. Seu treinador observa, a cada 10 minutos, o espaço percorrido e anota em uma tabela seu desempenho. Observe:
Exemplo: Numa esteira ergométrica, um atleta treina com uma velocidade constante para uma maratona. Seu treinador observa, a cada 10 minutos, o espaço percorrido e anota em uma tabela seu desempenho. Observe:
| Instante (minutos) | Distância (m) |
| 10 | 1 500 |
| 20 | 3 000 |
| 30 | 4 500 |
| 40 | 6 000 |
| 50 | 7 500 |
| 60 | 9 000 |
A cada instante (x), em minutos, corresponde a uma única distância (y), em metros. Dizemos então que a distância percorrida pelo atleta encontra-se em função do instante de tempo gasto em seu treinamento. Como a cada 10 minutos são percorridos 1500 metros; a cada minuto, 150 metros são percorridos, assim a fórmula que relaciona espaço e tempo pode ser descrita por y = 150x.
DEFINIÇÃO DE FUNÇÃO
Dados dois conjuntos A e B não vazios, uma função f de A em B é uma relação que associa a cada elemento x∈A , um único elemento y∈B . Assim, uma função liga um elemento do domínio (conjunto A de valores de entrada) com um segundo conjunto, o contradomínio (conjunto B de valores de saída) de tal forma que a cada elemento do domínio está associado exatamente a um, e somente um, elemento do contradomínio. O conjunto dos elementos do contradomínio que são relacionados pela f a algum x do domínio é o conjunto imagem, denotado por Im(f).
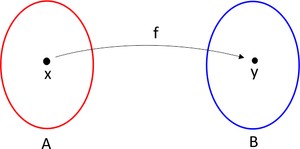
Vejamos um exemplo através da representação por diagramas, onde podemos observar a definição descrita:
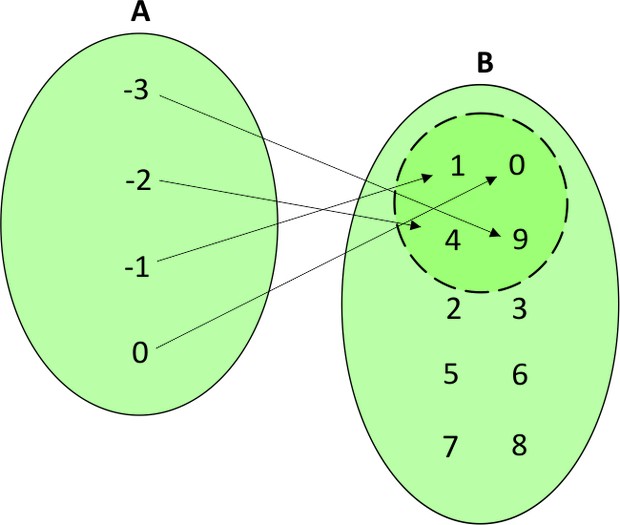
Representação por diagramas:
Cada elemento do conjunto A (domínio da função) está relacionado a um, e somente um, elemento do conjunto B (contradomínio da função). Todos os elementos do conjunto B que receberam flechas de A são imagens dos elementos de A, ou seja, a imagem de -3 é 9, imagem de -2 é 4, imagem de -1 é 1 e imagem de 0 é 0. Podemos perceber, nesse caso, que a imagem de cada elemento do conjunto A equivale ao quadrado do seu valor. Logo, podemos concluir que a lei de formação dessa função pode ser definida por f(x) = x².
Dom (f) = {-3,-2,-1,0}
CD (f) = {0,1,2,3,4,5,6,7,8,9}
IM (f) = {0,1,4,9}
CD (f) = {0,1,2,3,4,5,6,7,8,9}
IM (f) = {0,1,4,9}
Exemplo: Quais dos seguintes diagramas representam uma função de A em B?
 a)
a)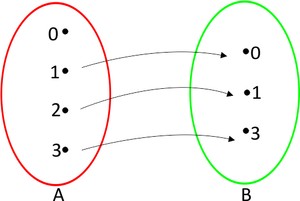 b)
b)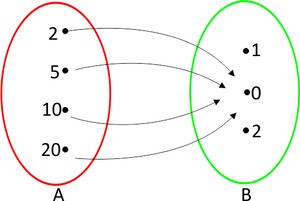 c)
c)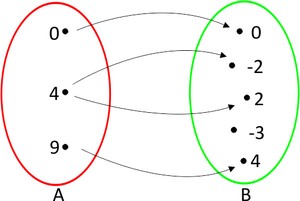 d)
d)De acordo com a definição de função apresentada anteriormente, os gráficos que representam funções são as letras: a e c. Consequentemente, os que não representam são as letras b e d, pois no item b o elemento 0 do conjunto A não se relacionou com nenhum elemento do conjunto B, contrariando a definição de função. Já na letra D, o elemento 4 do conjunto A se conectou com dois elementos do conjunto B, o que também não pode.
Observação: o que podemos concluir, caros alunos? Que cada elemento do conjunto A deve mandar uma e somente uma flecha para o conjunto B para a relação se tornar uma função. Jamais um elemento do conjunto A pode mandar 2 flechas ou deixar de mandar.
Exemplo: vamos entender melhor o que significa o domínio D e a imagem Im observando o gráfico abaixo:
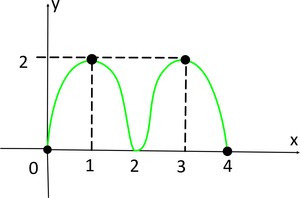
De acordo com que falamos acima, quando queremos saber sobre o domínio, devemos olhar para o eixo x e, quando falamos em imagem, devemos olhar pata o eixo y. Desse modo todos os valores utilizados sobre o eixo x representam o maior domínio dessa função, ou seja, D=[0,4] e todos ou valores utilizados sobre o eixo y representam a imagem, o que podemos concluir Im=[0,2]
Exemplo: vamos determinar o maior domínio das funções abaixo:
1º) f(x) = 3x
Sabemos que o denominador de uma fração tem que ser diferente de zero, pois não existe divisão por zero. Nesse caso, temos que ter x≠ 0 para que 2x seja possível em IR
Lodo o domínio são os reais não nulos.
2º) f(x) = x−4−−−−−√
Sabemos que no conjunto dos números reais não existe raiz quadrada de número negativo.
Portanto, temos que ter x−4≥0 para que seja possível em IR
Daí, x−4≥0⟺x≥4
Logo, D(f) = [4, + ∞[
3º) f(x) = 1−x√x−2√
Nesse caso, devemos ter:
(I) 7−x≥0⟺−x≥−7⟺x≤7
(II)x−2>0⟺x>2
(II)
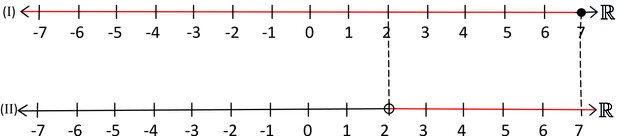
Ou seja, x∈ ]2, 7]. Para cada x∈ ]2, 7], f(x) existe e é único.
Logo, D(f) = ]2, 7].
Vamos observar agora mais um exemplo cotidiano onde a função se faz presente:
Uma barraca de praia, em Salvador, vende picolés ao preço de R$ 1,75 a unidade. Para não precisar fazer contas a todo momento, o proprietário da barraca montou a seguinte tabela:
| Número de picolés | Preço (R$) |
| 1 | 1,75 |
| 2 | 3,50 |
| 3 | 5,25 |
| 4 | 7,00 |
| 5 | 8,75 |
| 6 | 10,50 |
| 7 | 12,25 |
| 8 | 14,00 |
Note que o número de picolés é o domínio da função, e o preço correspondente à quantidade de picolés, o contradomínio. Logo, podemos observar que:
Dom (f) = {0,1,2,3,4,5,6,7,8}
CD (f) = {1,75; 3,50; 5,25; 7. 8,75; 10,5; 12,25; 14}
Im (f) = {1,75; 3,50; 5,25; 7. 8,75; 10,5; 12,25; 14}
Como todos os elementos do contradomínio são imagens, podemos concluir que o conjunto imagem é igual ao conjunto contradomínio.
Sendo assim, é possível observar facilmente a lei de formação dessa função. O total (y) a ser pago será R$ 1,75 multiplicado pela quantidade (x) de picolés. Logo, podemos concluir que y = 1,75.x.
Observação:
Seja f : R → R uma função. Tal representação pode ser descrita por D → CD onde D são os elementos do domínio e CD elementos do contradomínio. Sendo I o conjunto imagem, podemos dizer que I é subconjunto de CD, ou seja, I⊂ CD.
Classificação de uma função:
As funções podem ser classificadas em injetora ou injetiva, sobrejetora ou sobrejetiva e bijetora ou bijetiva. Uma função é:
- Injetora ou injetiva quando, para quaisquer elementos x1 ≠ x2 , temos f(x1 ) ≠ f(x2 );
- Exemplo:
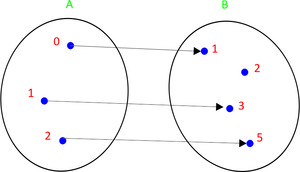
- Sobrejetora ou sobrejetiva quando o conjunto imagem for igual ao conjunto do contradomínio, ou seja, possuem os mesmos elementos;
Exemplo:
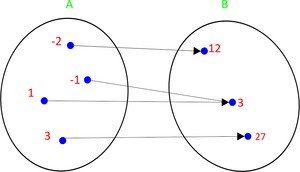 Funções (Foto: Colégio Qi)
Funções (Foto: Colégio Qi)
- Bijetora ou bijetiva quando ela for injetora e sobrejetora simultaneamente.
Exemplo:
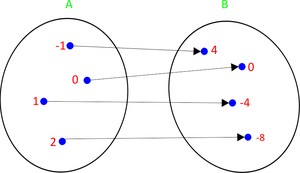 Funções (Foto: Colégio Qi)
Funções (Foto: Colégio Qi)
Assinar:
Comentários (Atom)
-
A função bijetora, também chamada de bijetiva, é um tipo de função matemática que relaciona elementos de duas funções. Desse modo, os ele...
-
Função é uma expressão matemática que relaciona dois valores pertencentes a conjuntos diferentes, mas com relações entre si. A lei de form...




